ÁNGULOS
Un ángulo es la parte del plano comprendida entre dos semirrectas que tienen el mismo punto de origen o vértice. Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.
Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
POR SU ABERTURA:
| Tipos de ángulos | Descripción | |
|---|---|---|
| Ángulo agudo | un ángulo de menos de 90° | |
| Ángulo recto | un ángulo de 90° | |
| Ángulo obtuso | un ángulo de más de 90° pero menos de 180° | |
| Ángulo llano | un ángulo de 180° | |
| Ángulo reflejo o cóncavo | un ángulo de más de 180° |
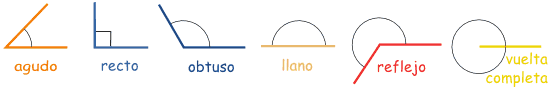
Cuidado con las medidas
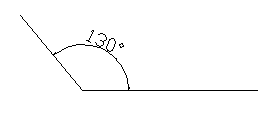 |  |
Este ángulo es obtuso.
|
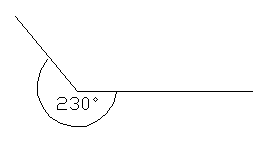
Este ángulo es reflejo.
|
POR SU POSICIÓN ENTRE PARALELAS Y UNA SECANTE (TRANSVERSAL):
Observa en el dibujo que dos rectas paralelas cortadas una recta transversal crea 8 ángulos que reciben distintos nombres según la posición que ocupan:
Las recta r corta a las rectas paralelas m y n:
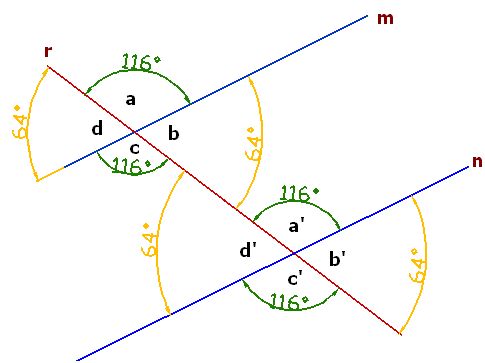
Los nombres de los ángulos según el lugar que ocupan reciben los nombres:
Interiores o internos:
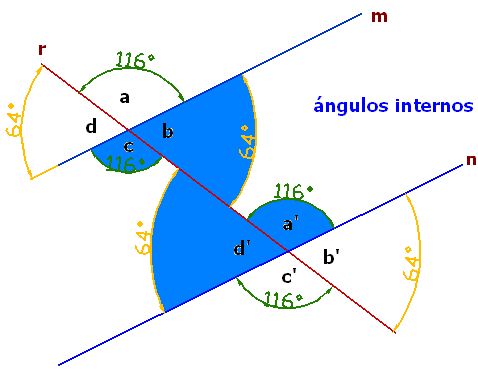
En azul, son los que se encuentran entre las rectas paralelas.
Ángulos exteriores o externos:

Los ángulos exteriores o externos en color violeta, son los que hallan en la zona exterior de las paralelas.
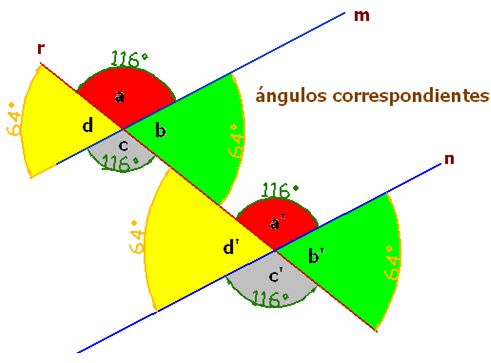
Ángulos correspondientes:
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Los ángulos del mismo color son correspondientes:
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
El ángulo a se corresponde con el ángulo a’
El ángulo b se corresponde con el ángulo b’
El ángulo c se corresponde con el ángulo c’
El ángulo d se corresponde con el ángulo d’
Teniendo en cuenta lo dicho hasta aquí y fijándonos en la figura podemos afirmar que los ángulos correspondientes son iguales entre sí.
Ángulos alternos internos
Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas:
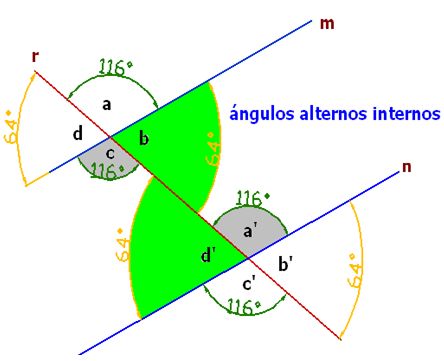
Los ángulos internos son d’, c, b y a’. Si los tomamos alternadamente, tendríamos, por un lado, los ángulos d’ y b, y por otro, c y a’ y comprobarás que los alternos internos son iguales entre sí.
Ángulos alternos externos:
Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas:
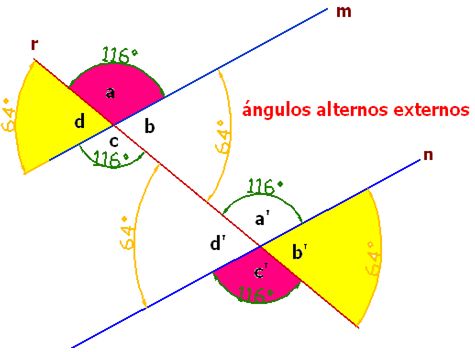
Los ángulos externos son: a, b’, c’ y d que tomándolos alternadamente tendremos, por un lado los ángulos a y c’, y por otro, los ángulos b’ y d. Comprobarás que los ángulos alternos externos son iguales entre sí.
*Observa la figura siguiente y después, contesta a las preguntas siguientes:
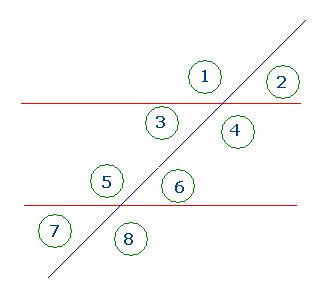
- ¿Cómo son los ángulos 1 y 2?
- ¿Cómo podemos llamar a los ángulos 1 y 4?
- ¿Son suplementarios los ángulos 2 y 4?
- ¿Son iguales los ángulos 2 y 3? ¿Por qué?
- ¿Son correspondientes los ángulos 3 y 7?
- ¿Cómo son los ángulos 4 y 6?
- ¿Es el ángulo 6 correspondiente al ángulo 3?
- ¿Son iguales los ángulos 5 y 8? ¿Por qué?
- ¿Cómo puedes llamarles a los ángulos 1 y 8?
- ¿Son alternos internos los ángulos 5 y 6?
POR LA SUMA DE SUS MEDIDAS:
 | Ángulos complementarios: dos ángulos son complementarios si suman 90° |
 | Ángulos suplementarios: dos ángulos son suplementarios si suman 180°. |
No hay comentarios:
Publicar un comentario